Geometrie und Basteln

Herbst 2010 mit DaLuJo

Winter 2014 mit Jo

  • Farbige Holzwürfel: Ein Haus gebaut
  • Wir messen die Seitenlängen und schreiben cm auf. Fläche in cm2
  • Zum Messen des Umfangs nehmen wir die Schnur zu Hilfe.
  • wir messen auch den Umfang mit der Schnur des Holzklötzliwagens.
  • Nun kommt der Würfel: Seitenlängen, Fläche in cm3
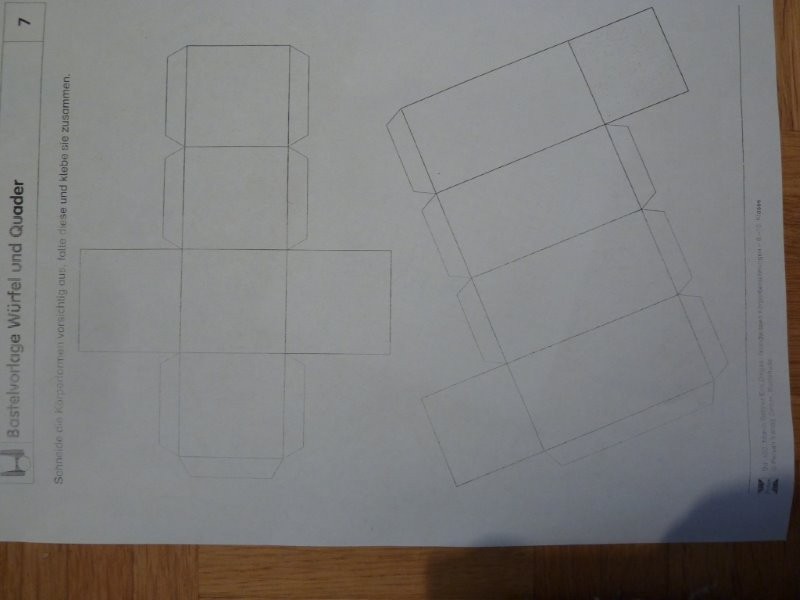
  • Vorlage zum Ausschneiden von Würfel und Quader
  • Würfel mit Schere ausschneiden und
  • und verleimen
  • Aufschreiben, was wir herausgefunden haben

Würfelkörper

Würfelkörper selber herstellen zur Veranschaulichung von Geometrie.

Download
Geometrie: Halbkarton schneiden und falzen
Geometrie falzen.wmv
Windows Media Video Format 5.7 MB
Download

Falten als Zugang zum Geometrieunterricht

Faltgeometrie

 

Ein Grossteil der Schulgeometrie lässt sich durch Faltgeometrie nachvollziehen.

 «Papierfalten ist mehr als ein blosses Falten und knicken. […] Wird ein Stück Papier gefaltet, so ist die Faltlinie eine Gerade. Faltet man ein weiteres Mal, sodass die soeben entstandene Faltlinie auf sich zu liegen kommt, wird eine Senkrechte zu den Geraden erzeugt…

 

 

Wer faltet, steckt unversehens inmitten der Geometrie! Die Kunst des Faltens ist ein hervorragender Zugang zum Geometrieunterricht. Wer faltet, braucht Auge, Hirn und Handfertigkeit. Falten fördert Einsicht, Verstehen und Begreifen!» (vgl. Quak 1998: 47)
Aus Faltlinien entstehen Figuren der Ebene, diese wiederum lassen sich zu Körpern zusammensetzen. Aus der Ebene entsteht durch Einsicht, Verstehen und Begreifen Raum…
«Origami ist ein traditionelles Faltspiel, in dem bildnerisch-ästhetische, funktionelle und geometrisch- mathematische Prinzipien zusammen fliessen.»

Quelle: obige Website

 

Millimeterpaper zum Falzen und Zeichnen f. Geometrie

Millimeterpapier zum selber ausdrucken

 

 

Geobrett

Ein Geobrett selber herstellen

 

 
Aus dem Internet kopiert:
Dieses webquest wurde für eine erste Klasse erstellt, die mit dem Umgang mit Geobrettern bereits vertraut war, so dass wir auf eine Einführung verzichtet haben. Die Begriffe `Spiegeln´ und `Spiegelstraße´werden durch Skizzen verdeutlicht.

 

Material:
Zum Bauen der Geobretter (4x4) werden pro Kind 16 Nägel und ein 12 x 12 cm großes und ca. 3cm dickes Weichholzbrett sowie Hammer und Schmirgelpapier und eine Kopie des Bauplans benötigt.
Zum späteren Arbeiten mit den Brettern sind mindestens 3 bunte Gummiringe pro Kind nötig.

 

Zum Erstellen der Kartei werden Tonkartonblätter in A5 benötigt. Diese kann man durch Laminieren haltbar machen oder in Klarsichthüllen aufbewahren. Vordrucke der Geobretter für die Karten können entweder von den Schülern ausgedruckt oder kopiert den Kinder zur Verfügung gestellt werden.

Um den Schülern den Ablauf zu erleichtern, haben wir pro Gruppentisch Laufkarten vorbereitet, auf denen die Reihenfolge der Arbeitsaufträge kurz beschrieben ist und die Kinder zur Kontrolle ihre erledigten Aufgaben abhaken können.

 

Verwendung auch für spätere Schuljahre Mittel-/Oberstufe: 

Platonische Körper, Tetraeder, Hexaeder, Oktaeder, Ikosaeder, Dodekaeder darstellen